Магнитной цепью называют совокупность тел или сред, по которым замыкается магнитный поток.
Для любого участка магнитной цепи можно получить выражение, устанавливающее связь между магнитным потоком, МДС, действующей в данной цепи, а также ее геометрическими размерами, пользуясь понятием магнитного потока и законом полного тока.
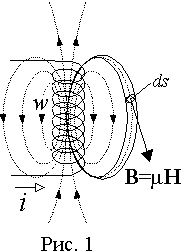
Пусть имеется цилиндрическая катушка с числом витков w, по которым протекает ток i (рис. 1). Выделим трубку магнитного потока, охватывающую все витки катушки, и определим МДС вдоль ее контура
|
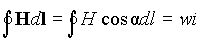 , ,
|
(1)
|
но в изотропной среде направление векторов B и H совпадает. Поэтому вектор H направлен по касательной к оси трубки и cosa =1. Отсюда
|
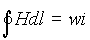 . .
|
(2)
|
В тоже время, элементарный магнитный поток, проходящий через сечение перпендикулярное оси трубки, и напряженность магнитного поля равны
|
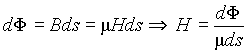 . .
|
(3)
|
Подставим полученное выражение для напряженности в выражение (2) и с учетом того, что элементарный поток dФ вдоль трубки имеет постоянное значение, получим
|
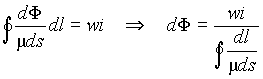 . .
|
(4)
|
Если распространить приведенные рассуждения на весь магнитный поток катушки, то при условии, что размеры сечений магнитных трубок существенно меньше их длины, из выражения (4) будем иметь:
|
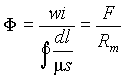 , ,
|
(5)
|
где величина 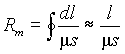 называется магнитным сопротивлением. В этом выражении m - абсолютная магнитная проницаемость среды; l - длина средней линии, т.е. линии проходящей через центр поперечного сечения магнитопровода s. Магнитное сопротивление измеряется в [Гн-1] называется магнитным сопротивлением. В этом выражении m - абсолютная магнитная проницаемость среды; l - длина средней линии, т.е. линии проходящей через центр поперечного сечения магнитопровода s. Магнитное сопротивление измеряется в [Гн-1]
В выражении (5) магнитный поток Ф связан с МДС F и магнитным сопротивлением Rm аналогично тому, как связаны между собой электрический ток, ЭДС и сопротивление в выражении закона Ома. Однако сходство между этими законами чисто формальное, т.к. они существенно различаются между собой. Электрическое сопротивление может быть бесконечно большим и в этом случае возможно существование ЭДС без протекания электрического тока в цепи. Магнитное сопротивление всегда конечно и наличие МДС означает одновременное обязательное существование магнитного потока.
ЗАДАЧА 1
ЗАДАЧА 2
Обычно для расчета магнитных цепей применяют закон полного тока. Если разбить магнитную цепь на участки так, чтобы в пределах каждого из них площадь поперечного сечения и магнитная среда были одинаковыми, то можно считать, что магнитный поток проходит по каждому участку вдоль его средней линии. При этом индукция в пределах каждого участка будет постоянной, следовательно, постоянной будет и напряженность магнитного поля. Тогда в левой части выражения (2) интеграл вдоль замкнутого контура, проходящего по средним линиям сечений всех участков магнитной цепи, можно представить суммой
|
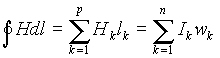 , ,
|
(6)
|
где p - число участков магнитной цепи длиной l, в пределах которых H=const; n - число обмоток, охватываемых средней линией контура, с числом витков w и током I.
Произведение Hl=Uм называется магнитным падением напряжения или магнитным напряжением, а Iw=F является МДС. Пользуясь этими понятиями, можно представить выражение (6) в форме аналогичной второму закону Кирхгофа для электрических цепей
т.е. сумма падений магнитного напряжения вдоль замкнутого контура магнитной цепи равна алгебраической сумме МДС катушек, охватываемых контуром.
Однако следует заметить, что Г.Р.Кирхгоф этот закон не формулировал и он является формальной аналогией.
ЗАДАЧА 3
Другой формальной аналогией законам Кирхгофа, вытекающей из принципа непрерывности магнитного потока, является равенство нулю алгебраической суммы магнитных потоков в узлах магнитной цепи.
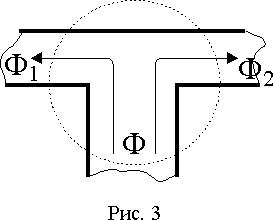
Например, если магнитопровод разделяется на части (рис. 3), то разделяется на составляющие Ф1 и Ф2 магнитный поток Ф. Поскольку магнитный поток через любую замкнутую поверхность равен нулю, то окружив разветвление магнитопровода такой произвольной поверхностью получим
|
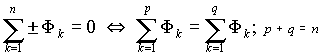
|
(8)
|
Первая запись соответствует некоторому соглашению о знаках магнитных потоков. Например, можно считать потоки направленные к узлу положительными, а от узла отрицательными. Вторая запись объединяет в левую и правую части равенства потоки с одинаковой ориентацией.
Следует заметить, что выражение (8) справедливо только при условии, что магнитный поток не ответвляется через боковые поверхности магнитопровода в окружающую среду.
Понятие магнитного сопротивления можно использовать для расчетов магнитных цепей с ферромагнетиками только в том случае, если вещество ненасыщено, т.к. в противном случае входящее в него значение магнитной проницаемости m зависит от Ф.
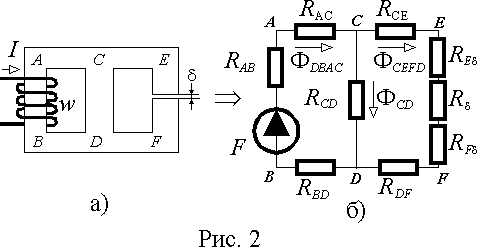
Если разбить магнитную цепь (рис 2 а)) на участки с одинаковой площадью поперечного сечения и веществом, то каждый такой участок можно представить магнитным сопротивлением в соответствии с выражением (5). Катушку с током I можно представить МДС равной F=Iw.
В результате этих преобразований, исходная магнитная цепь будет представлена электрической схемой замещения (рис. 2 б)), в которой роль токов будут играть магнитные потоки на соответствующих участках. К этой схеме формальной можно применить все законы и методы расчета электрических цепей.
ЗАДАЧА 4
При расчете магнитной цепи с ферромагнетиком в общем случае нужно иметь данные о геометрических размерах и материале магнитопровода. Задача расчета может формулироваться в двух вариантах, называемых прямой и обратной задачей. В первом случае по заданному на каком-либо участке магнитному потоку или индукции нужно определить МДС, необходимую для создания этого потока. В обратной задаче по заданной МДС нужно определить магнитный поток или индукцию на каком-либо участке.
Обратная задачи существенно отличаются от прямой, т.к. может быть решена только методом последовательных приближений.
При расчетах магнитных цепей обычно делают следующие допущения:
- весь магнитный поток проходит по магнитопроводу, не ответвляясь в окружающую среду, т.е. пренебрегают т.н. потоком рассеяния;
- в воздушных зазорах пересекающих магнитопровод отсутствует выпучивание магнитных линий, т.е. поперечное сечение магнитного потока в зазорах считают равным сечению магнитопровода.
Рассмотрим магнитную цепь, приведенную на рис. 4 а). Пусть для этой цепи требуется определить МДС обмотки, обеспечивающую в воздушном зазоре cd магнитный поток с плотностью Bcd =1,5 Тл. Геометрические размеры магнитопровода приведены в таблице 1.
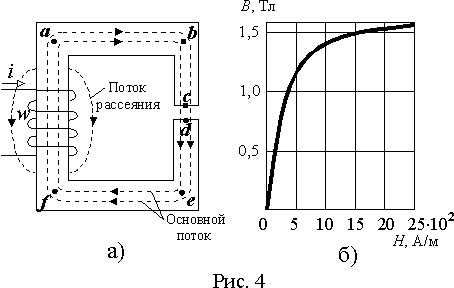
Потоком рассеяния мы пренебрегаем и считаем, что весь магнитный поток замыкается по магнитопроводу из ферромагнетика, кривая намагничивания которого приведена на рис. 4 б).
Разобьем магнитопровод на участки с одинаковыми площадями поперечного сечения, что обеспечит выполнение условия H=const в пределах каждого участка.
По заданной площади поперечного сечения магнитопровода на участках bc и de найдем значение магнитного потока в зазоре как Ф = Bcd Scd = 1,5Ч 1,0Ч 10-4 = 1,5Ч 10-4 Вб.
Для участков bc и de, имеющих сечение равное воздушному зазору, плотность магнитного потока будет равна заданной плотности в зазоре, а для участков ab , ef и af определим плотность как отношение потока Ф к площади поперечного сечения соответствующего участка.
Для воздушного зазора магнитная проницаемость m является константой. Поэтому для любого воздушного промежутка напряженность магнитного поля H в А/м однозначно определяется через индукцию (плотность магнитного потока) B в Тл в виде
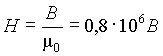 . .
Далее для всех участков магнитопровода по значению плотности магнитного потока B с помощью кривой намагничивания рис. 4 б) определим напряженность магнитного поля H и, умножив ее на длины соответствующих участков найдем падения магнитного напряжения. Результаты этих вычислений сведены в таблицу.
Таблица 1.
|
Участок
|
S
ґ 10-4[м2]
|
L
ґ 10-3 [м]
|
B=Ф/S
[Тл]
|
H
[А/м]
|
Hl=Uм
[А]
|
|
ab
|
1,5
|
50
|
1,0
|
700
|
35
|
|
bc
|
1,0
|
" 40
|
1,5
|
1500
|
60
|
|
cd
|
|
1
|
1,5
|
1,2Ч 106
|
1200
|
|
de
|
1,0
|
40
|
1,5
|
1500
|
60
|
|
ef
|
1,5
|
50
|
1,0
|
700
|
35
|
|
fa
|
1,5
|
80
|
1,0
|
700
|
56
|
|
Iw=
|
1460
|
Таким образом, для создания магнитного потока плотностью в 1,5 Тл в воздушном зазоре толщиной в 1 мм нужна обмотка, в которой произведение силы тока на число витков равно 1460 АЧ витков. Причем, как следует из таблицы 1, на проведение потока по всему магнитопроводу с длиной средней линии 260 мм требуется только 18% МДС, а остальные 82% необходимы для создания потока в воздушном зазоре, т.е. воздушный зазор определяет необходимую минимальную МДС.
ЗАДАЧА 5
Обратная задача расчета магнитной цепи, т.е. определение магнитного потока или индукции по заданному значению МДС обмотки, решается методом последовательных приближений, когда произвольно задаются значением искомого магнитного потока и решают прямую задачу, находя соответствующую МДС. Если она не соответствует заданной, изменяют значение потока и снова решают прямую задачу. Итерационный процесс повторяют до получения удовлетворительного совпадения расчетной МДС с заданной.
Решим задачу определения индукции в воздушном зазоре магнитной цепи рис. 4 а) при МДС катушки равной 1000 А. Результаты расчетов, начиная с индукции 1,0 Тл с шагом 0,1 приведены в таблице 2.
Таблица 2.
|
B
[Тл]
|
Ф
ґ 10-4[Вб]
|
Ucd
[А]
|
Ubafe
[А]
|
Ubc
[А]
|
F
[А]
|
|
1,0
|
0,66(6)
|
800
|
45
|
24
|
869
|
|
1,1
|
0,73(3)
|
880
|
54
|
36
|
970
|
|
1,2
|
0,8
|
920
|
61
|
40
|
1021
|
Аппроксимируя интервал между 1,1 и 1,2 Тл, получим для МДС 1000 А плотность магнитного потока 1,158 Тл.
Источник: https://de.ifmo.ru/--books/electrotech/mc/mc_7.htm | 










