| Меню сайта |
|
 |
| Категории раздела |
|
 |
| Статистика |
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
 |
|
Параметрический резонанс
-
Параметрический резонанс - явление раскачки колебаний при периодич. изменении параметров тех элементов колебат. системы, в к-рых сосредоточивается энергия колебаний (реактивные или энергоёмкие параметры). П. р. возможен в колебат. системах различной физ. природы. Напр., в колебательном контуре реактивными параметрами явл. ёмкость Си индуктивность L, в к-рых запасены электрич. энергия Wэ=q2/2C и магн. энергия Wм=LI2/2 (q — заряд наобкладках конденсатора, I — ток в катушке индуктивности). Собств. колебания в контуре без потерь спостоянными С и L происходят с частотой w0=1/?LC. При этом полная энергия W=Wэ+Wм, запасённая вконтуре, остаётся неизменной, происходит лишь её периодич. трансформация из электрич. в магнитную иобратно с частотой 2w0. Изменение параметров С и L, сопровождающееся затратой работы внеш. сил(накачка), приводит к изменению полной энергии системы. Если ёмкость С изменить скачком (за время, малоепо сравнению с периодом собств. колебаний Т0=2p/w0) (рис. 1, а), то заряд q скачком
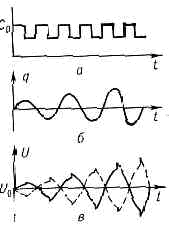
Рис. 1. Связь между изменениями ёмкости С конденсатора (а), заряда q на его обкладках (б) и напряжения U(в) при параметрич. резонансе в колебат. контуре.
измениться не может (иначе ток I=aq/dt®?, рис.1, б). В результате напряжение на ёмкости U=q/C и электрич. энергия Wэ=q2/2C изменяются обратно пропорц. С, причём совершаемая при этом работа пропорц. q2. Если изменять ёмкость С периодически в такт сизменениями Wэ (обусловленными собств. колебаниями), уменьшая её в моменты, когда ?q? и Wэмаксимальны, и увеличивая, когда эти величины равны нулю (рис. 1), то в среднем за период над системойсовершается работа и, следовательно, полная энергия и амплитуда колебаний будут монотонно нарастать.
Раскачка колебаний возможна при изменении С или L по любому периодич. закону с периодом Тн иличастотой wн, определяемыми соотношениями:
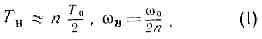
где n — целое число. Наиболее эфф. раскачка имеет место при n=1, когда частота накачки wн равна частотеколебаний Wэ и Wм в системе w0. Нарастание колебаний возможно не только при точном выполнениисоотношения (1), но и в нек-рых конечных интервалах значений wн вблизи w0 (в зонах неустойчивости), ширина зон тем больше, чем сильнее изменяются параметры С и L. Изменение параметра, напр. ёмкости С, характеризуют величиной m=(Cмакс-Cмин)/(Cмакс+Cмин) наз. глубиной изменения параметра (рис. 2).
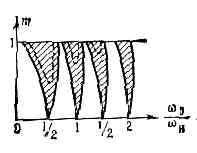
Рис. 2. Области значений m, в к-рых возможен параметрич. резонанс; w0 — частота собств. колебаний, wн — частота накачки (изменения параметра).
П. р. приводит к нарастанию малых нач. возмущений, напр. Неизбежных во всякой системе флуктуации, средик-рых всегда найдётся составляющая с подходящей фазой по отношению к фазе изменения параметров, т. е. к самовозбуждению колебаний. В отсутствии потерь энергии самовозбуждение наступает при сколь угодномалом изменении параметров. Если же в системе имеются потери (напр., в контуре присутствуетсопротивление Л), то самовозбуждение происходит только при достаточно больших изменениях С или L, когдапараметрич. накачка энергии превосходит потери. Зоны неустойчивости при этом соответственноуменьшаются или даже исчезают совсем (при больших потерях). Нарастание колебаний при П. р. непроисходит беспредельно, а ограничивается при достаточно больших амплитудах разл. нелинейнымиэффектами. Напр.: зависимость сопротивления Л от тока в контуре может приводить к увеличению потерь помере возрастания амплитуды колебаний, а зависимость ёмкости от напряжения на ней — к изменениюпериода собств. колебаний Т0 и в результате — к увеличению расстройки между значениями wн и w0/2n. Равновесие наступает тогда, когда параметрич. накачка энергии в среднем за период компенсируетсяджоулевыми потерями (см. ПАРАМЕТРИЧЕСКАЯ ГЕНЕРАЦИЯ И УСИЛЕНИЕ ЭЛЕКТРОМАГНИТНЫХКОЛЕБАНИЙ).

Рис. 3. а — устройство маятника с переменной длиной l подвеса; б — схема движения тела маятника за одинпериод.
Пример механич. системы, в к-рой возможен П. р.,— маятник в виде груза массы т, подвешенного на нити, длину l к-рой можно изменять (рис. 3). Маятник с неподвижной точкой подвеса совершает собств. колебания счастотой w0=?G/L, причём сила натяжения нити (равная по величине сумме центробежной силы исоставляющей силы тяжести, направленной вдоль нити) максимальна в нижнем положении груза иминимальна в крайних. Поэтому если уменьшать l в нижнем и увеличивать в крайних положениях (при этомснова выполняется соотношение (1)), то работа внеш. силы, совершаемая в среднем за период, оказываетсяположительной и колебания могут раскачиваться. На П. р. основано самораскачивание на качелях, когда эфф. длина маятника периодически изменяется при приседаниях и вставаниях качающегося. П. р. учитывается внебесной механике при расчёте возмущений планетных орбит, вызванных влиянием др. планет.
В колебат. системах с неск. степенями свободы (напр., в системе из двух связанных контуров, маятников идр.) возможны нормальные колебания (моды) с разл. частотами w1, w2. Поэтому колебания энергии, запасённой в к.-л. реактивном элементе, содержат не только составляющие с частотами 2w1, 2w2, но и счастотами, равными суммам и разностям разл. нормальных частот. Соответственно нарастание колебанийздесь возможно как при выполнении условия (1) для любой из норм. частот, так и, напр., при изменениипараметра с суммарной частотой:
wн =w1+w2. (2)
П. р. приводит к самовозбуждению обоих норм. колебаний с определ. соотношением фаз. Резонансная связьмод возможна также при wн=w1-w2, однако при этом вместо самовозбуждения происходит лишь периодич. перекачка энергии между модами. Соотношение (2) выражает закон сохранения энергии при распаде кванта«накачки» с энергией ћw на два кванта: ћw1 и ћw2. Отсюда следует также, что мощность Рн, поступающая вколебат. систему на частоте wн, и мощности P1,P2 потребляемые на частотах w1 и w2, пропорц. соответствующим частотам (частный случай т. н. соотношений Мэнли — Роу):
Pн/wн=P1/w1=P2/w2 (3)
В колебат. системах с распределёнными параметрами, обладающих бесконечным числом степеней свободы, также возможно возбуждение норм. колебаний в результате П. р. Классич. пример — опыт Мельде (1859), в к-ром наблюдалось возбуждение поперечных колебаний (стоячих волн) в струне, прикреплённой одним концом кножке камертона, колебания к-рого периодически меняют натяжение струны (рис. 4) с частотой, вдвоебольшей частоты собств. поперечных колебаний. П. р. может приводить к раскачке изгибных колебанийвращающихся валов. Др. пример — опыт Фарадея (1831), в к-ром вертикальные колебания сосуда с водойприводят к возбуждению стоячей поверхностной волны с удвоенным периодом.
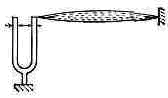
Рис. 4. Параметрич. возбуждение колебаний струны.
Существенная особенность П. р. в системах с распределёнными параметрами состоит в том, что егоэффективность зависит от соотношения между законом изменения параметров системы в пр-ве ипространств. структурой колебаний (волн). Напр., если накачка, изменяющая параметры среды, представляетсобой бегущую волну с частотой wн и волновым вектором kн, то возбуждение пары норм. волн с частотамиw1, w2 и волн. векторами k1, k2 осуществляется, если выполняются условия П. р. как во времени, так и в пр-ве:
wн=w1+w1; kн=k1+k2. (4)
На квант. языке эти условия, обобщающие (2), означают, что при распаде кванта накачки сохраняются какэнергия, так и импульс (ћk). Нарастание амплитуд волн во времени и пр-ве (распадная неустойчивость) такжеограничивается нелинейными эффектами: если значит. часть энергии накачки израсходована на возбуждениеэтих волн, то возможен обратный процесс — рост энергии накачки за счёт ослабления волн на частотах w1, w2; в среде без потерь такой обмен энергией происходит периодически. Параметрические и нелинейныерезонансные вз-ствия волн характерны, напр., для разл. типов волн в плазме, мощных световых волн (см. ПАРАМЕТРИЧЕСКИЙ ГЕНЕРАТОР СВЕТА), волн в электронных пучках и др. волн. процессов.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
-
ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС
-
- явлениераскачки колебаний при периодич. изменении параметров тех элементов колебат. <системы, в к-рыхсосредоточивается энергия колебаний (реактивные или энергоёмкиепараметры). П. р. возможен в колебат. системах разл. физ. природы. Напр.,в электрич. колебательном контуре реактивными параметрамиявляютсяёмкость С и индуктивность L, в к-рых запасены электрич. энергия W э = q2/2C и магн. энергия W м = LI2/2 (где q - заряд на обкладках конденсатора,I - ток в катушке индуктивности). Собств. колебания в контуребезпотерь с постоянными С и L происходят с частотой 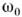 = 1/LC. При этом полная энергия W = W э+ Wм,запасённая в контуре, остаётся неизменной, происходит лишь её периодич. <трансформация изэлектрической в магнитную и обратно с частотой = 1/LC. При этом полная энергия W = W э+ Wм,запасённая в контуре, остаётся неизменной, происходит лишь её периодич. <трансформация изэлектрической в магнитную и обратно с частотой 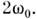 Изменение параметров С и L, сопровождающеесяработой внеш. <сил (накачка), приводит к изменению полной энергии системы. Если ёмкость . изменитьскачком за время, малое по сравнению с периодом собств. колебаний Изменение параметров С и L, сопровождающеесяработой внеш. <сил (накачка), приводит к изменению полной энергии системы. Если ёмкость . изменитьскачком за время, малое по сравнению с периодом собств. колебаний 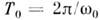 (рис. 1, а), то зарядскачком измениться не может (поскольку силатока I остаётся конечной величиной, рис. 1,б). Врезультатенапряжение на ёмкости U = q/C (рис. 1, в) и электрич. энергияW, изменяются обратно пропорц. С, причём совершаемая при этом работапропорц. q2. Если изменять ёмкость С периодическив такт изменениямW э, (обусловленным собств. колебаниями),уменьшая её в моменты, когда q2 и W э максимальны, <иувеличивая, когда эти величины равны нулю (рис. 1), то в ср. за периоднад системой совершается положит. работа и, следовательно, полная энергияи амплитуда колебаний будут монотонно нарастать. (рис. 1, а), то зарядскачком измениться не может (поскольку силатока I остаётся конечной величиной, рис. 1,б). Врезультатенапряжение на ёмкости U = q/C (рис. 1, в) и электрич. энергияW, изменяются обратно пропорц. С, причём совершаемая при этом работапропорц. q2. Если изменять ёмкость С периодическив такт изменениямW э, (обусловленным собств. колебаниями),уменьшая её в моменты, когда q2 и W э максимальны, <иувеличивая, когда эти величины равны нулю (рис. 1), то в ср. за периоднад системой совершается положит. работа и, следовательно, полная энергияи амплитуда колебаний будут монотонно нарастать.
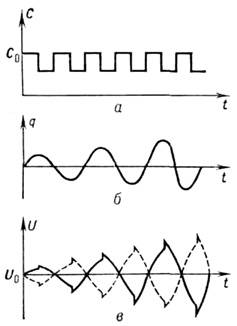
Рис. I. Связь между изменениями ёмкости С конденсатора ( а), заряда q на его обкладках ( б )и напряжения U(в )при параметрическом резонансе в колебательномконтуре.
П. р. наиб. эффективно проявляется приизменении параметров колебат. системы с периодом Т н,кратнымполупериоду собств. колебаний Т0:
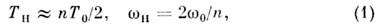
где п - целое число,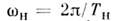 - частота накачки. Математически свободные колебания в таких системахописываютсядифференц. ур-ниями с переменными коэф. Напр., в случае колебат. контурас перем. ёмкостьюC(t )(в отсутствие омического сопротивления) ур-ниеотносительно заряда q(l )имеет вид - частота накачки. Математически свободные колебания в таких системахописываютсядифференц. ур-ниями с переменными коэф. Напр., в случае колебат. контурас перем. ёмкостьюC(t )(в отсутствие омического сопротивления) ур-ниеотносительно заряда q(l )имеет вид
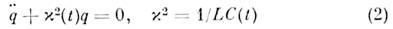
(ур-ние Xилла). Согласно Флоке теореме, общее решение (2) можно записать в виде
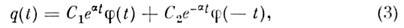
где С 1,2 - произвольныекоэф., определяемые нач. условиями,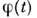 - периодич. ф-ция с периодом Т н - периодич. ф-ция с периодом Т н 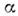 - коэф., зависящий от параметров системы. При выполнении условия (1) - коэф., зависящий от параметров системы. При выполнении условия (1)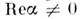 и один из членов (3) даётнарастающие во времени колебания. Наиб. быстраяраскачка имеет место при п =1, когда частота накачки и один из членов (3) даётнарастающие во времени колебания. Наиб. быстраяраскачка имеет место при п =1, когда частота накачки 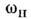 равна частоте колебаний величин W о и WM всистеме равна частоте колебаний величин W о и WM всистеме 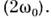 Нарастание колебаний возможно не толькопри точном выполнении соотношений(1), но и в нек-рых конечных интервалах значений Нарастание колебаний возможно не толькопри точном выполнении соотношений(1), но и в нек-рых конечных интервалах значений 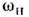 вблизи вблизи 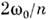 (взонах неустойчивости), ширина зон тем больше, чем сильнее изменяютсяпараметры С и L. Изменениепараметра, напр. ёмкости С, характеризуютвеличиной (взонах неустойчивости), ширина зон тем больше, чем сильнее изменяютсяпараметры С и L. Изменениепараметра, напр. ёмкости С, характеризуютвеличиной
т= (Смакс - С мин)/(Cмакс + Cмин),
наз. глубиной изменения параметра. В частномслучае синусоидального изменения 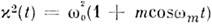
[ур-ние (2) при этом наз. ур-нием Матьё]в осн. зоне ( п= 1) при т 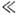 1 инкремент 1 инкремент 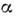 равен равен
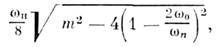
так что в середине зоны 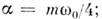 во второй зоне ( п=2) во второй зоне ( п=2)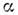 ~ m2, в третьей ~ m2, в третьей 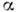 ~ т 3 и т. д. ~ т 3 и т. д.
П. р. приводит к неустойчивости колебат. <системы, т. е. к нарастанию малых нач. возмущений, напр. неизбежных вовсякой системе флуктуаций, среди к-рых всегда найдётся составляющая с подходящейфазойпо отношению к фазе изменения параметров. В отсутствие потерь энергиипараметрич. неустойчивостьнаступает при сколь угодно малой глубине измененияпараметров. Если же в системе имеются потери (напр., вконтуре присутствуетсопротивление R), то неустойчивость возникает только при достаточнобольшихизменениях С или L, когда параметрич. накачка энергиипревосходит потери. Зоны неустойчивости приэтомсоответственноуменьшаются или даже исчезают совсем (на рис. 2) уменьшать l в нижнем и увеличивать вкрайних положениях [при этом снова выполняетсясоотношение (1)], то работа внеш. силы, совершаемая в ср. за период, оказываетсяположительной и колебания могут раскачиваться. На П. р. основаносамораскачиваниена качелях, когда эфф. длина маятника периодически изменяется при приседанияхивставаниях качающегося. П. р. учитывается в небесной механике при расчётевозмущений планетных орбит, вызванных влиянием др. планет.
В колебат. системах с неск. степенямисвободы (напр., в системе из двух связанных контуров, маятников идр.)возможны нормальные колебания (моды) с разя, частотами 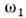 , ,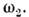 Поэтому колебания энергии, запасённой в к.-л. реактивном элементе, содержатне только составляющие с частотами Поэтому колебания энергии, запасённой в к.-л. реактивном элементе, содержатне только составляющие с частотами 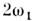 . .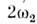 ,но и счастотами, равными суммам и разностям разл. нормальных частот. Соответственнонарастание колебанийздесь возможно как при выполнении условия (1) длялюбой из нормальных частот, так и, напр., при изменениипараметра с суммарнойчастотой: ,но и счастотами, равными суммам и разностям разл. нормальных частот. Соответственнонарастание колебанийздесь возможно как при выполнении условия (1) длялюбой из нормальных частот, так и, напр., при изменениипараметра с суммарнойчастотой:
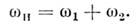
П. р. приводит к самовозбуждению обоихнормальных колебаний с определ. соотношением фаз. Резонанснаясвязь модвозможна также при 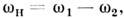 однако при этом вместо самовозбуждения происходит лишьпериодич. перекачкаэнергии между модами. Соотношение (2) выражает закон сохранения энергиипри распадекванта "накачки" с энергией однако при этом вместо самовозбуждения происходит лишьпериодич. перекачкаэнергии между модами. Соотношение (2) выражает закон сохранения энергиипри распадекванта "накачки" с энергией 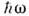 на два кванта: на два кванта: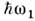 и и 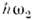 .Отсюда следует также, что мощность Р н, поступающая вколебат. систему на частоте .Отсюда следует также, что мощность Р н, поступающая вколебат. систему на частоте 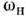 ,и мощности Р1, Р 2, потребляемые начастотах ,и мощности Р1, Р 2, потребляемые начастотах 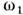 и и 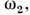 пропорц. <соответствующим частотам (частный случай т. н. соотношений Мэнли - Роу): пропорц. <соответствующим частотам (частный случай т. н. соотношений Мэнли - Роу):
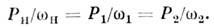
В колебат. системах с распределёнными параметрами, <обладающих бесконечным числом степеней свободы, также возможно возбуждениенормальных колебаний в результате П. р. Классич. пример - опыт Мельде(1859),в к-ром наблюдалось возбуждение поперечных колебаний (стоячих волн) в струне, <прикреплённойодним концом к ножке камертона, колебания к-рого периодическименяют натяжение струны (рис. 4) счастотой, вдвое больше частоты собств. <поперечных колебаний. П. р. может приводить к раскачке изгибныхколебанийвращающихся валов. Др. пример - опыт Фарадея (1831), в к-ром вертикальныеколебания сосуда сводой приводит к возбуждению стоячей поверхностной водыс удвоенным периодом.
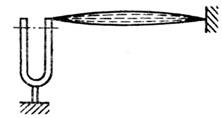
Рис. 4. Параметрическое побуждение колебанийструны.
Существ. особенность П. р. в волновых системахсостоит в том, что его эффективность зависит отсоотношения между закономизменения параметров системы в пространстве и пространственнойструктуройволи. Напр., если накачка, изменяющая параметры среды, представляет собойбегущую волну счастотой 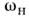 и волновым вектором kH, то возбуждение пары нормальныхволн с частотами и волновым вектором kH, то возбуждение пары нормальныхволн с частотами 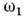 , ,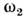 иволновыми векторами k1, k2 осуществляется, <если выполняются условия П. р. как во времени, так и впространстве: иволновыми векторами k1, k2 осуществляется, <если выполняются условия П. р. как во времени, так и впространстве:
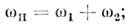 kH = k+ k2. (4) kH = k+ k2. (4)
В предельном случае бесконечно большойфазовой скорости волны накачки 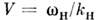 (k н (k н  0приконечном 0приконечном 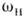 ) условия (4) дают k2 ) условия (4) дают k2 - k1, и в простейшем случае - k1, и в простейшем случае 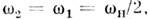 т. е. нарастать можетстоячая волна на половинной частоте. В другом предельномслучае ( т. е. нарастать можетстоячая волна на половинной частоте. В другом предельномслучае (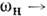 0 при конечном k н, 0 при конечном k н,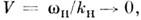 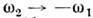 )равенства (4) сводятся к условию резонансного (брэггов-ского) отраженияот неподвижной периодич. неоднородности среды; здесь полная энергия сигналаостаётсяпостоянной, а происходит его отражение (непропускание) периодич. <структурой. )равенства (4) сводятся к условию резонансного (брэггов-ского) отраженияот неподвижной периодич. неоднородности среды; здесь полная энергия сигналаостаётсяпостоянной, а происходит его отражение (непропускание) периодич. <структурой.
На квантовом языке условия (4) означают, <что при распаде кванта накачки сохраняются как энергия, так иимпульс 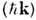 .Нарастание амплитуд волн во времени и в пространстве (распадная неустойчивость)такжеограничивается нелинейными эффектами: если значит. часть энергиинакачки израсходована на возбуждениеэтих волн, то возможен обратный процесс- рост энергии накачки за счёт ослабления волн на частотах .Нарастание амплитуд волн во времени и в пространстве (распадная неустойчивость)такжеограничивается нелинейными эффектами: если значит. часть энергиинакачки израсходована на возбуждениеэтих волн, то возможен обратный процесс- рост энергии накачки за счёт ослабления волн на частотах 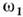 , ,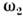 ; в среде без потерь такой обмен энергией происходит периодически. ; в среде без потерь такой обмен энергией происходит периодически.
Возможны также многоволновые процессы, <когда во взаимодействии участвует большее число волн.
Параметрич. и нелинейные резонансные взаимодействияволн характерны, напр., для разл. типов волн вплазме, мощных световыхволн (см. Параметрический генератор света), волн в электронных пучкахи др. волновых процессов.
Лит.: Мандельштам Л. И., Лекциипо теории колебаний, М., 1972; Основы теории колебаний, 2 изд., М., 1988;Рабинович М. И., Трубецков Д. И., Введение в теорию колебаний и волн, М.,1984.
Л. А. Островский, Н. С. Степанов.
|
|
Категория: Из Сети | Добавил: rakarskiy (13.11.2017) W |
| Просмотров: 1180
| Рейтинг: 0.0/0 |
|
|
| Вход на сайт |
|
 |
| Поиск |
|
 |
| Друзья сайта |
|
 |
|











