https://www.cbseguess.com/ebooks/xii/physics/mutual-induction.php

Когда поток, создаваемый переменным током в одной катушке (обычно называемой первичной), соединяется с тесно расположенной катушкой (называемой вторичной), говорят, что взаимная индукция.

Если I ₂ - ток, протекающий во вторичной обмотке, то потоковые связи с первичной катушкой пропорциональны току во вторичной катушке. То есть,

где M ₁₂ - взаимная индуктивность первичной по отношению к вторичной. Он также называется коэффициентом взаимной индукции. Аналогично, если I1 - ток, протекающий в первичной обмотке, то потоковые связи со вторичной катушкой пропорциональны току в первичной обмотке. То есть,

где M ₂₁ - взаимная индуктивность вторичной по отношению к первичной. Он также называется коэффициентом взаимной индукции.

Взаимная индуктивность двух круговых коаксиальных концентрических катушек:

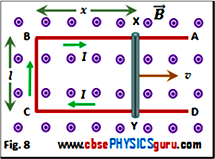
Пусть r ₁ и r ₂ (r ₁ << r ₂ ) - радиусы двух коаксиальных концентрических катушек, а N ₁ и N ₂ - количество витков в двух катушках. См. Рисунок 14. Пусть вторичная (внешняя) катушка переносит ток I ₂ . Магнитное поле в центре за счет тока I ₂ дается формулой

Поскольку первичная (внутренняя) коаксиальная катушка имеет очень малый радиус, B ₂ можно считать постоянной по площади поперечного сечения первичной. Следовательно, полные потоковые связи с первичной (внутренней) катушкой даются выражением

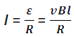
Но, N ₁ Φ ₁ = M ₁₂ I ₂ . Поэтому взаимная индуктивность первичной по отношению к вторичной дается выражением

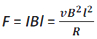
Нелегко вычислить флюсовую связь со вторичной (внешней) катушкой, так как магнитное поле, обусловленное первичной (внутренней) катушкой, изменяется поперек поперечного сечения вторичной катушки. Поэтому расчет M ₂₁ также будет чрезвычайно сложным в этом случае. Равенство M ₁₂ = M ₂₁ = M (скажем), заданное теоремой взаимности, очень полезно в таких ситуациях. Следовательно, взаимная индуктивность вторичной по отношению к первичной дается формулой

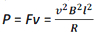
Взаимная индуктивность двух коаксиальных соленоидов:

Пусть r ₁ и r ₂ - радиусы внутреннего (пусть это первичные P) и внешние (пусть это вторичные S) коаксиальные соленоиды соответственно, а n ₁ и n ₂ - количество витков на единицу длины двух соленоидов. Пусть N ₁ и N ₂ - общее число витков в двух соленоидах и каждая длина l. См. Рисунок 15.

Пусть вторичный соленоид несут ток I ₂ . Этот ток устанавливает магнитный поток Φ ₁ через первичный (внутренний) соленоид. Полные потоковые связи с первичным соленоидом приведены в виде N ₁ Φ ₁ = M ₁₂ I ₂

где M ₁₂ - взаимная индуктивность первичного (внутреннего) соленоида относительно вторичного (внешнего) соленоида.

Магнитное поле в центре вторичного соленоида, обусловленное током I ₂ , определяется как B ₂ = μ ₀ n ₂ I ₂

Общие потоковые связи с первичным соленоидом даются формулой

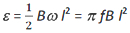
Но, N ₁ Φ ₁ = M ₁₂ I ₂ . Поэтому взаимная индуктивность первичной по отношению к вторичной дается выражением

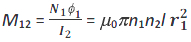
Точно так же полные потоковые связи со вторичным соленоидом из-за тока в первичной области определяются N ₂ Φ ₂ = (n ₂ l) B ₁ A ₁

Здесь следует отметить, что мы используем A ₁ вместо A ₂ . Поток из-за тока I ₁ во внутреннем соленоиде можно считать ограниченным только внутри этого соленоида (т.е. первичного), поскольку соленоиды очень длинные и, следовательно,

N ₂ Φ ₂ = (n ₂ l) B ₁ A ₁ (μ ₀ Πn ₁ n ₂ / r ₁ ² ) / 1

Но N ₂ Φ ₂ = M ₂₁ I ₁ . Следовательно, взаимная индуктивность вторичной по отношению к первичной дается формулой

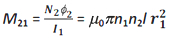
Ясно, что M ₁₂ = M ₂₁ = M (скажем)

Здесь следует отметить, что это равенство справедливо только для длинных коаксиальных соленоидов. Поэтому для длинных коаксиальных соленоидов

M = μ ₀ Πn ₁ n ₂ / r ₁ ²

Важно также отметить, что взаимная индуктивность пары катушек, соленоидов и т. Д. Зависит от их разделения, а также от их относительной ориентации.

https://www.electronicshub.org/inductors-in-parallel/

Содержание 
1 Индукторы, соединенные параллельно (без магнитной муфты)

1.1. Пример индукторов, подключенных параллельно

2 Взаимозависимые индукторы в параллельном

2.1 Параллельные вспомогательные индукторы

2.2 Пример параллельных вспомогательных индукторов

2.3 Параллельные противолежащие индукторы

2.3.1 Пример параллельных противоположных индукторов

3 Резюме

 Как известно, индукторы соединены параллельно, когда два контакта индуктора соответственно соединены с каждым выводом других индукторов или индуктора. Подобно параллельному соединению резисторов, общая индуктивность в параллельном соединении индукторов несколько меньше, чем наименьшая индуктивность индуктора в этом соединении.
Индукторы в параллельных

 Когда индукторы соединены параллельно, ток через каждый индуктор не точно равен суммарному току, но сумма каждого отдельного тока через параллельные индукторы дает полный ток (поскольку он делит между параллельными индукторами).
Если ток через каждый индуктор меньше общего тока, магнитное поле, генерируемое каждым индуктором, также меньше, чем ток поля, генерируемого полным током через него.
В случае резисторов параллельно большая часть тока протекает через наименьший резистор, поскольку он обеспечивает наименьшую оппозицию потоку тока, чем больший резистор.
Аналогично, если индукторы подключены параллельно, ток выбирает наименьший путь оппозиции индуктора, когда ток в этой схеме уменьшается или увеличивается, когда каждый индуктор индивидуально выступает против этого изменения (увеличение или уменьшение тока).
Индуктор параллельно с эквивалентом
В параллельном соединении напряжение на каждом индукторе равно, а также при изменении общего тока падение напряжения на каждом отдельном индукторе будет меньше по сравнению с последовательным подключением. При заданной скорости изменения тока меньше будет индуктивность при меньшем напряжении.
Это основные моменты, которые следует учитывать при параллельном соединении индукторов. Теперь мы обсудим параллельное соединение индукторов с учетом взаимной связи между этими индукторами и без них.
Индукторы, подключенные параллельно (без магнитной муфты)Как мы обсуждали выше, один конец индукторов соединен с узлом, а другие концы индукторов соединены вместе с другим узлом в параллельном соединении. Параллельное соединение n индукторов показано на рисунке ниже.
Учтите, что магнитная связь между индукторами отсутствует и, следовательно, полная индуктивность равна сумме обратных величин индивидуальных индуктивностей. Давайте обсудим, как это утверждение можно получить.
Индуктор параллельно без взаимной индуктивности
Мы знаем, что в параллельной сети напряжение остается постоянным, а ток делится на каждый параллельный индуктор. Если I L1 , I L2 , I L3 и т. Д. I Ln - индивидуальные токи, протекающие в параллельно соединенных индукторах L 1 , L 2 и т. Д. Соответственно L n , то полный ток в параллельных индукторах задается формулой
I Итого = I L1 + I L2 + I L3 . , , , + I n
Если отдельные падения напряжения в параллельном соединении являются V L1 , V L2 , V L3 и так далее V Ln , то общее падение напряжения между двумя терминалами V T является
V Всего = V L1 = V L2 = V L3 . , , , = V n
Падение напряжения в терминах самоиндукции может быть выражено как V = L di / dt. Это подразумевает полное падение напряжения,
V T = L T di / dt
⇒ L T  d / dt (I L1 + I L2 + I L3 ... + In)
⇒ L T ((d i1 ) / dt + (d i2 ) / dt + (d i3 ) / dt ...)
Подставляя V / L вместо di / dt, приведенное выше уравнение становится
V T = L T (V / L 1 + V / L 2  + V / L 3  ...)
Поскольку падение напряжения является постоянным по всей цепи, то V = V T . Поэтому мы можем написать
1 / L T = 1 / L 1 + 1 / L 2  + 1 / L 3  . , , , ,
Это означает, что обратная полная индуктивность параллельного соединения представляет собой сумму обратных величин индивидуальных индуктивностей всех индукторов. Вышеприведенное уравнение верно, когда взаимная индуктивность не влияет на параллельные соединенные катушки.
Чтобы избежать сложностей при работе с фракциями, мы можем использовать метод продукта по сумме для вычисления полной индуктивности. Если два индуктора соединены параллельно, и если между ними нет взаимной индуктивности, то полная индуктивность задается как
L T = (L 1 × L 2 ) / (L 1 + L 2 )
Пример индукторов, подключенных параллельноЕсли схема имеет 2 индуктора 20 Генри и 30 Генри, соединенных параллельно, какова будет полная индуктивность параллельного расположения?
Sol: Мы знаем, что формула для полной индуктивности рядов, 1 / L T = 1 / L 1 + 1 / L 2
Учитывая, что L 1 = 20 Генри
L 2 = 30 Генри
L T = (L 1 * L 2 ) / (L 1 1+ L 2 ) = ((20 * 30)) / ((20 + 30)) = 600/50 = 12
Полная индуктивность равна L Total = 12 Henry.
Взаимозависимые индукторы в параллельномКогда существует магнитная связь между индукторами, приведенная выше производная формула для полной индуктивности должна быть изменена, поскольку полная индуктивность может быть более или менее в зависимости от направлений магнитного поля от каждого индуктора. Магнитный поток, создаваемый параллельно соединенными индукторами, будет связываться друг с другом.
Когда генерируемые потоки находятся в одном и том же направлении магнитного потока, взаимная индуктивность будет возрастать; эти катушки называются «вспомогательными» катушками. Если поток находится в противоположном направлении к магнитному потоку, взаимная индуктивность будет уменьшаться; эти катушки называются «противостоящими» катушками. Эта взаимная индуктивность будет зависеть от установленного расстояния двух катушек.
Рассмотрим, что два индуктора соединены параллельно с собственными индуктивностями L 1 и L 2 и которые взаимно связаны с взаимной индуктивностью M, как показано на рисунке ниже.
Индуктор параллельно с пособничеством и противодействием
Параллельные вспомогательные индукторыРассмотрим фигуру (а), в которой индукторы L 1  и L 2 соединены параллельно с их поддержкой магнитных полей. Полный ток через схему определяется как
i = i 1 + i 2
di / dt = (di 1 ) / dt + (di 2 ) / dt ............. (1)
Напряжение на индукторе или параллельной ветви задается как
V = L 1 (di 1 ) / dt + M (di 2 ) / dt или L 2 (di 2 ) / dt + M (di 1 ) / dt
L 1 (di 1 ) / dt + M (di 2 ) / dt = L 2 (di 2 ) / dt + M (di 1 ) / dt
(di 1 ) / dt (L 1 - M) = (di 2 ) / dt (L 2 - M)
(di 1 ) / dt = (di 2 ) / dt ((L 2 - M)) / ((L 1 - M)) ............. (2)
Подставляя уравнение 2 в уравнение 1, получим
di / dt = (di 2 ) / dt ((L 2 - M)) / ((L 1 - M)) + (di 2 ) / dt
di / dt = (di 2 ) / dt {(L 2 - M)) / ((L 1 - M)) + 1} ............. (3)
Если L T - полная индуктивность схемы параллельного индуктора, то напряжение определяется выражением
V = L T di / dt
L T di / dt = L 1 (di 1 ) / dt + M (di 2 ) / dt
di / dt = 1 / L T {L 1 (di 1 ) / dt + M (di 2 ) / dt}
Подставляя уравнение 2 в уравнение выше, получим
di / dt = 1 / L T {L 1 (di 2 ) / dt (L 2 - M)) / ((L 1 - M)) + M (di 2 ) / dt}
di / dt = 1 / L T {L 1 (L 2 - M)) / ((L 1 - M)) + M} (di 2 ) / dt ............. (4)
Приравнивая уравнения 3 и 4, получим
(L 2 - M)) / ((L 1 - M)) + 1 = 1 / L T {L 1 (L 2 - M)) / ((L 1 - M)) + M}
Упрощение приведенного выше уравнения, результаты
L T = (L 1 L 2 - M 2 ) / (L 1 + L 1 ) -2M)
Здесь 2M представляет собой магнитный поток L 1 на L 2 или L 2 на L 1 . Если величина двух индуктивностей равна идеальной магнитной связи между ними, эквивалентная индуктивность двух индукторов равна L, так как L T = L 1 = L 2 = M. В таком случае, если взаимная индуктивность равна нулю, полная индуктивность будет L ÷ 2.
Пример параллельных вспомогательных индукторовЕсли два индуктора 25mH и 45mH подключены параллельно, вычислите полную индуктивность параллельной комбинации. Взаимодействующая индуктивность задается как 20 мГн.
SolGiven, что L 1 = 25 мГн
L 2 = 45 мГн
M = 20 мГн
Применяя формулу для полной индуктивности вспомогательных индукторов, L T = (L 1 L 2 - M 2 ) / (L 1 + L 1 ) -2M)
L Т = (25 * 20 45- 2 ) / (25 + 45-2 * 20)
= (1125-400) / (70-40)
= 725/30
= 24,166 мМ
Поэтому полная индуктивность составляет 24.166 миллион Генри.
Параллельные противолежащие индукторыАналогично, если мы рассмотрим цифру (b), в которой индукторы L 1 и L 2 соединены параллельно с их противоположными магнитными полями, полная индуктивность задается как
L T = (L 1 L 2 - M 2 ) / (L 1 + L 2 ) + 2M)
В противоположных параллельных индукторах, если величины двух индуктивностей равны идеальной магнитной связи, эквивалентная индуктивность двух индукторов будет равна нулю, так как они взаимно компенсируют друг друга. Если два индуктора эффективно пропускают ток через них, полная индуктивность задается как (L ± M) ÷ 2.
Пример параллельных противоположных индукторовПример: если два индуктора 25mH и 45mH подключены параллельно друг другу, вычислите полную индуктивность параллельной комбинации. Взаимодействующая индуктивность задается как 20 мГн.
Sol: Учитывая, что L 1 = 25 мГн
L 2 = 45 мГн
M = 20 мГн
Применяя формулу для полной индуктивности вспомогательных индукторов, L T = (L 1 L 2 M 2 ) / (L 1 + L 2 ) + 2M)
L T = (25 * 45-20 2 ) / (25 + 45 + 2 * 20)
= (1125-400) / (70 + 40)
= 725/110
= 6,59 мГн
Поэтому общая индуктивность составляет 6,59 милиГенри.
РезюмеПодсоединение двух клемм индуктора соответственно к другим контакторам индуктора или катушки индуктивности, то это соединение называется «параллельным соединением катушек индуктивности».Когда потоки, создаваемые отдельными индукторами, находятся в одном и том же направлении, взаимная индуктивность будет увеличена; то эти катушки называются «вспомогательными» катушками. Общая индуктивность для вспомогательных катушек L T = (L 1 L 2 - M 2 ) / (L 1 + L 2 ) -2M). Когда потоки, создаваемые отдельными индукторами, находятся в противоположном направлении магнитного потока, взаимная индуктивность будет уменьшаться; то эти катушки называются «противоположными» катушками. Общая индуктивность для вспомогательных катушек составляет L T = (L 1 L 2 - M 2 ) / (L 1 + L 2 ) + 2M)

*****

Inductors series [Серия индукторов]

         Индуктор - это пассивный элемент, который используется в электронных схемах для временного хранения электрической энергии в виде магнитного потока или просто магнитного поля. Индуктивность - это свойство любой катушки, которая может настраивать магнитный поток, когда ток проходит через него.
Любое устройство, обладающее свойством индуктивности, можно назвать индуктором. Обычно индуктор построен в виде катушки с медным материалом вокруг сердечника магнитной (железной) или немагнитной среды (например, воздуха).

        Индукторы могут быть подключены последовательно или параллельно, зависит от характеристик, требуемых схемой. Эти комбинации используются для разработки более сложных сетей. Полная индуктивность цепи зависит от того, как подключаются индукторы, может быть как последовательно, так и параллельно.
       Кроме того, как индукторы связаны так, что одна индуктивность не влияет на другую, также изменяется общая индуктивность по сравнению с действием магнитной связи между индукторами.
Поэтому индукторы расположены на основе их взаимной индуктивности или магнитной связи последовательно или параллельно.

Индукторы, соединенные в серии

        Предположим, что индукторы, подключенные в цепи, не имеют никакой связи между ними. Это означает, что нет линий потока от одного индуктора, соединяющегося с другим, и, следовательно, между катушками не будет взаимного потока.
       Соединение от конца до конца двух или более индукторов называется «последовательным соединением индукторов». В связи с этим индукторы соединены последовательно, поэтому эффективные витки индуктора возрастают. Последовательное соединение индукторов показано на диаграмме ниже

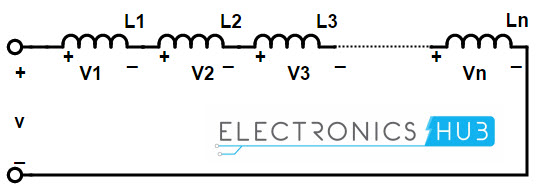
        Индуктивность последовательно соединенных индукторов рассчитывается как сумма индивидуальных индуктивностей каждой катушки, так как изменение тока через каждую катушку одинаково.
         Это последовательное соединение аналогично соединению последовательно соединенных резисторов, за исключением того, что резисторы заменяются индукторами. Если ток I протекает в последовательном соединении, а катушки - L1, L2 и т. Д., Общий ток в индукторах серии задается формулой
                   I Итого = I L1 = I L2 = I L3 . , , = I n
Если индивидуальное напряжение падает на каждую катушку в этом соединении серии VL1, VL2, V¬L3 и т. Д., Общее падение напряжения между двумя клеммами VT дается формулой
                  V Всего = V L1 + V L2 + V L3 .... + V n
Как мы знаем, падение напряжения может быть представлено в терминах собственной индуктивности L, это означает
                     V = L di / dt.
Это также можно записать в виде
                     LT di / dt = L1 di / dt + L2 di / dt + L3 di / dt +. , , + Ln di / dt
Поэтому полная индуктивность
                    L Всего = L 1 + L 2 + L 3 + ... .. + L n
Это означает, что полная индуктивность последовательного соединения представляет собой сумму индивидуальных индуктивностей всех индукторов. Вышеприведенное уравнение верно, когда нет взаимной индуктивности между катушками в этой конфигурации серии.
Взаимная индуктивность индукторов приведет к изменению значения полной индуктивности в последовательной комбинации индукторов.
         Предположим, что есть два индуктора, соединенных последовательно с источником переменного напряжения, который может генерировать переменный ток в цепи, как показано на приведенном выше рисунке.
              Если в цепи нет взаимной индуктивности, то полная индуктивность дается как
                   L T = L 1 + L 2
Важно помнить, что полная индуктивность всегда больше, чем наибольшая индуктивность в последовательном расположении индукторов.
Индукторы, подключенные в серии Пример

Пример 1: Если схема имеет 3 индуктора 60 Генри, 30 Генри и 20 Генри, соединенных последовательно, какова будет общая индуктивность серии?
Сол: Мы знаем, что формула полной индуктивности серии, L Total = L 1 + L 2 + L 3 + ... .. + L n
Учитывая, что L 1 = 60 Генри
L 1 = 30 Генри
L 1 = 20 Генри
Полная индуктивность, L Всего = 60 + 30 + 20 = 110 Генри.

Взаимозависимые индукторы в сериях

     Теперь рассмотрим, что индукторы соединены таким образом, что магнитное поле одной катушки влияет на другое. Когда два или более индуктора соединены последовательно, на индуктивность одного индуктора будет влиять магнитное поле, создаваемое другой катушкой.
       Это называется взаимной индуктивностью, а катушки называются «взаимозависимыми индукторами». Эта взаимная индуктивность может увеличить или уменьшить общую индуктивность серии.
Коэффициент, влияющий на взаимную индуктивность ряда, связанного индукторами, - это расстояние между катушками и их ориентацией.
Связанные друг с другом индукторы могут соединяться двумя типами
1) Кумулятивно связанная или серия Aiding
2) Дифференциально связанные или Серии противостоящие

Кумулятивно связанные индукторы в серии

Если магнитные потоки, создаваемые индукторами, находятся в одном направлении с потоком тока через них, то катушки известны как «кумулятивно связанные».
В этой серии вспомогательной или кумулятивной связанной цепи ток входит или выходит из клемм катушек в любой момент времени в одном направлении.
На рисунке ниже показано соединение двух индукторов в последовательном порядке.

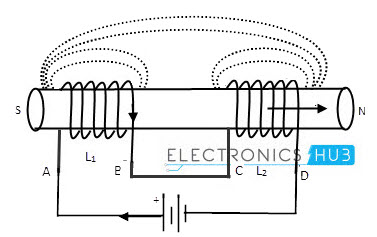
     Если мы пропускаем ток через кумулятивно связанные катушки (между узлами A & D) в одном направлении, падение напряжения каждой отдельной катушки будет влиять на общую индуктивность серии.
     Пусть самоиндукция катушки-1 равна L 1 , самоиндукция катушки-2 равна L 2, а взаимная индуктивность равна M между катушкой 1 и катушкой2.
Самовозбуждаемая эдс в катушке-1
e1 = - L 1 di / dt
Взаимная индуцированная э.д.с. в катушке-1 из-за изменения тока в катушке-2
eM1 = - M di / dt
Аналогично, эмиссионная ЭДС в катушке-2
e2 = - L 2 di / dt
Взаимная индуцированная эдс в катушке-2 из-за изменения тока в катушке-1
eM2 = - M di / dt
Таким образом, суммарная индуцированная э.д.с. в цепи вспомогательного ряда приводится как
e = - L 1 di / dt-L 2 di / dt-2M di / dt
= - (L 1 + L 2 + 2M) di / dt
Если L T - полная индуктивность схемы, то суммарная индуцированная э.д.с. будет эквивалентна
e = - L T di / dt
Подставляя в вышеприведенное уравнение, получаем
- L T di / dt = - (L 1 + L 2 + 2M) di / dt
Поэтому L T = (L 1 + L 2 + 2M)

Кумулятивно связанные индукторы в серии Пример

Пример: если две катушки индуктивности 70 мГн и 30 мГн соединены последовательно, то найдите общую кумулятивную индуктивность последовательно соединенных индукторов. Рассмотрим взаимную индуктивность комбинации двух катушек 40 мГн.
Соль:
Учитывая, что L 1 = 70 мГн
L 2 = 30 мГн
М = 40 мГн
Применяя формулу для кумулятивно связанных индукторов, LT = L1 + L2 + 2M
L T = 70 + 30 + 2 (40)
= 100 + 80
= 180 мГн
Поэтому кумулятивная индуктивность катушки составляет 180 милиГенри.

Дифференциально связанные индукторы в сериях
Если магнитные потоки, создаваемые индукторами, находятся в противоположном направлении друг к другу, то катушки известны как «дифференциально связанные».
В этом дифференциальном соединении с последовательным или последовательным сопротивлением ток входит или выходит из клемм катушек в любой момент времени в противоположном направлении.
На рисунке ниже показано соединение двух индукторов в последовательном расположении оппозиции.

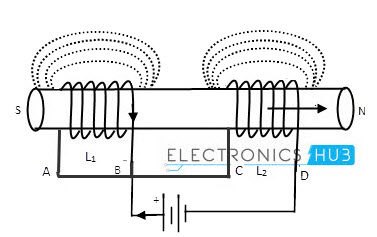
В дифференциально связанных катушках поля магнитного потока могут производиться в том же направлении или в противоположном направлении. Пусть сама индуктивность катушек L1 и L2, а взаимная индуктивность равна M.
Здесь взаимная индуктивность будет обеспечиваться каждой индуктивностью катушки из-за конфигурации схемы. Следовательно, суммарная индуцированная э.д.с. в цепи противоположного ряда дается как
e = - L 1 di / dt-L 2 di / dt + 2M di / dt
= - (L 1 + L 2 - 2M) di / dt
Если L T - полная индуктивность схемы, то суммарная индуцированная э.д.с. будет эквивалентна
e = - L T di / dt
Подставляя в вышеприведенное уравнение, получаем
- L T di / dt = - (L 1 + L 2 - 2M) di / dt
Поэтому L T = (L 1 + L 2 - 2M)
Дифференциально связанные индукторы в серии Пример
Пример: если две катушки индуктивности 70 мГн и 30 мГн подключены последовательно, то найдите полную дифференциальную индуктивность последовательно соединенных индукторов. Рассмотрим взаимную индуктивность комбинации двух катушек 40 мГн.
Соль:
Учитывая, что L 1 = 70 мГн
L 2 = 30 мГн
М = 40 мГн
Применяя формулу для дифференциально связанных индукторов, LT = L1 + L2 - 2M
L T = 70 + 30 - 2 (40)
= 100 - 80
= 20 мГн
Поэтому дифференциальная индуктивность катушки составляет 20 милиГенри.

 Резюме:

• Индуктор представляет собой пассивный элемент, который используется в электронных схемах для хранения энергии в виде магнитного потока. Индуктивность измеряется в Генри.
• Величина диссипации фактической мощности с током в цепи называется «Индуктивное сопротивление». Он измеряется в омах. X L = 2  f L
• Самоиндукция является свойством электрической цепи или петли, в которой ее собственное магнитное поле выступает против любого изменения тока
• Взаимная индуктивность - это способность индуктора, которая вызывает индуцирование ЭДС в другом индукторе, расположенном очень близко к нему, когда изменяется ток в первом индукторе.
• Соединение от конца до конца двух или более индукторов называется «последовательным соединением индукторов».
• Формула полной индуктивности в серии L T = L 1 + L 2
• Полная индуктивность последовательно соединенных индукторов всегда больше, чем наибольшая индуктивность в этой серии.
• Если магнитные потоки, создаваемые индукторами, находятся в одном направлении с потоком тока через них, то катушки известны как «кумулятивно связанные». L T = L 1 + L 2 + 2M
• Если магнитные потоки, создаваемые индукторами, находятся в противоположном направлении друг к другу, то катушки известны как «дифференциально связанные». L T = L 1 + L 2 - 2 M